The Solar System Guided Reading and Study Answers

A paper's "Methods" (or "Materials and Methods") section provides information on the study's design and participants. Ideally, it should be so clear and detailed that other researchers can repeat the study without needing to contact the authors. You will need to examine this section to determine the study's strengths and limitations, which both affect how the study's results should be interpreted.

Demographics

The "Methods" section usually starts by providing information on the participants, such as age, sex, lifestyle, health status, and method of recruitment. This information will help you decide how relevant the study is to you, your loved ones, or your clients.

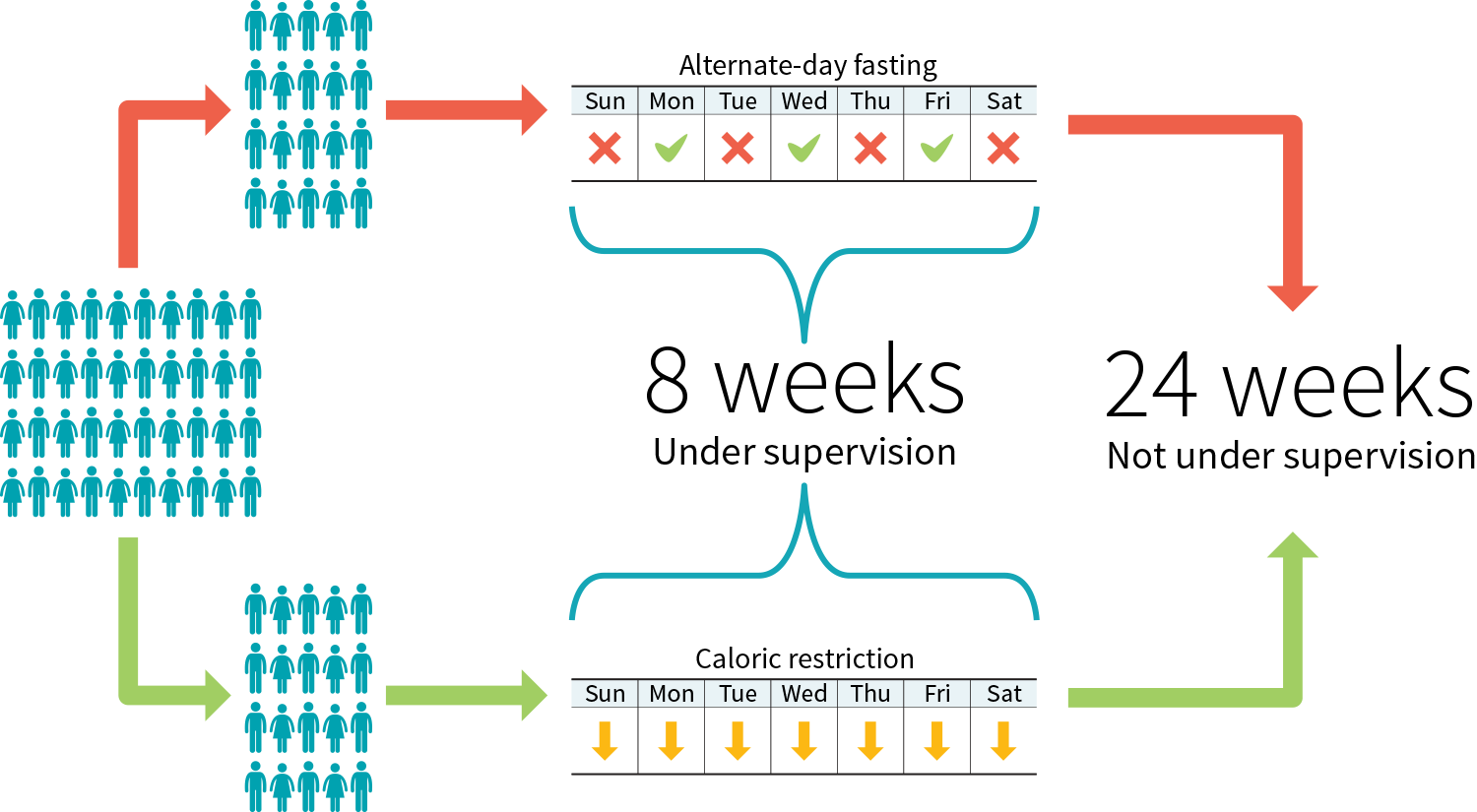
Figure 3: Example study protocol to compare two diets

The demographic information can be lengthy, you might be tempted to skip it, yet it affects both the reliability of the study and its applicability.

Reliability. The larger the sample size of a study (i.e., the more participants it has), the more reliable its results. Note that a study often starts with more participants than it ends with; diet studies, notably, commonly see a fair number of dropouts.

Applicability. In health and fitness, applicability means that a compound or intervention (i.e., exercise, diet, supplement) that is useful for one person may be a waste of money — or worse, a danger — for another. For example, while creatine is widely recognized as safe and effective, there are "nonresponders" for whom this supplement fails to improve exercise performance.

Your mileage may vary, as the creatine example shows, yet a study's demographic information can help you assess this study's applicability. If a trial only recruited men, for instance, women reading the study should keep in mind that its results may be less applicable to them. Likewise, an intervention tested in college students may yield different results when performed on people from a retirement facility.

Figure 4: Some trials are sex-specific

Furthermore, different recruiting methods will attract different demographics, and so can influence the applicability of a trial. In most scenarios, trialists will use some form of "convenience sampling". For instance, studies run by universities will often recruit among their students. However, some trialists will use "random sampling" to make their trial's results more applicable to the general population. Such trials are generally called "augmented randomized controlled trials".

Confounders

Finally, the demographic information will usually mention if people were excluded from the study, and if so, for what reason. Most often, the reason is the existence of a confounder — a variable that would confound (i.e., influence) the results.

For example, if you study the effect of a resistance training program on muscle mass, you don't want some of the participants to take muscle-building supplements while others don't. Either you'll want all of them to take the same supplements or, more likely, you'll want none of them to take any.

Likewise, if you study the effect of a muscle-building supplement on muscle mass, you don't want some of the participants to exercise while others do not. You'll either want all of them to follow the same workout program or, less likely, you'll want none of them to exercise.

It is of course possible for studies to have more than two groups. You could have, for instance, a study on the effect of a resistance training program with the following four groups:

• Resistance training program + no supplement

• Resistance training program + creatine

• No resistance training + no supplement

• No resistance training + creatine

But if your study has four groups instead of two, for each group to keep the same sample size you need twice as many participants — which makes your study more difficult and expensive to run.

When you come right down to it, any differences between the participants are variable and thus potential confounders. That's why trials in mice use specimens that are genetically very close to one another. That's also why trials in humans seldom attempt to test an intervention on a diverse sample of people. A trial restricted to older women, for instance, has in effect eliminated age and sex as confounders.

As we saw above, with a great enough sample size, we can have more groups. We can even create more groups after the study has run its course, by performing a subgroup analysis. For instance, if you run an observational study on the effect of red meat on thousands of people, you can later separate the data for "male" from the data for "female" and run a separate analysis on each subset of data. However, subgroup analyses of these sorts are considered exploratory rather than confirmatory and could potentially lead to false positives. (When, for instance, a blood test erroneously detects a disease, it is called a false positive.)

Design and endpoints

The "Methods" section will also describe how the study was run. Design variants include single-blind trials, in which only the participants don't know if they're receiving a placebo; observational studies, in which researchers only observe a demographic and take measurements; and many more. (See figure 2 above for more examples.)

More specifically, this is where you will learn about the length of the study, the dosages used, the workout regimen, the testing methods, and so on. Ideally, as we said, this information should be so clear and detailed that other researchers can repeat the study without needing to contact the authors.

Finally, the "Methods" section can also make clear the endpoints the researchers will be looking at. For instance, a study on the effects of a resistance training program could use muscle mass as its primary endpoint (its main criterion to judge the outcome of the study) and fat mass, strength performance, and testosterone levels as secondary endpoints.

One trick of studies that want to find an effect (sometimes so that they can serve as marketing material for a product, but often simply because studies that show an effect are more likely to get published) is to collect many endpoints, then to make the paper about the endpoints that showed an effect, either by downplaying the other endpoints or by not mentioning them at all. To prevent such "data dredging/fishing" (a method whose devious efficacy was demonstrated through the hilarious chocolate hoax), many scientists push for the preregistration of studies.

Sniffing out the tricks used by the less scrupulous authors is, alas, part of the skills you'll need to develop to assess published studies.

Interpreting the statistics

The "Methods" section usually concludes with a hearty statistics discussion. Determining whether an appropriate statistical analysis was used for a given trial is an entire field of study, so we suggest you don't sweat the details; try to focus on the big picture.

First, let's clear up two common misunderstandings. You may have read that an effect was significant, only to later discover that it was very small. Similarly, you may have read that no effect was found, yet when you read the paper you found that the intervention group had lost more weight than the placebo group. What gives?

The problem is simple: those quirky scientists don't speak like normal people do.

For scientists, significant doesn't mean important — it means statistically significant. An effect is significant if the data collected over the course of the trial would be unlikely if there really was no effect.

Therefore, an effect can be significant yet very small — 0.2 kg (0.5 lb) of weight loss over a year, for instance. More to the point, an effect can be significant yet not clinically relevant (meaning that it has no discernible effect on your health).

Relatedly, for scientists, no effect usually means no statistically significant effect. That's why you may review the measurements collected over the course of a trial and notice an increase or a decrease yet read in the conclusion that no changes (or no effects) were found. There were changes, but they weren't significant. In other words, there were changes, but so small that they may be due to random fluctuations (they may also be due to an actual effect; we can't know for sure).

We saw earlier, in the "Demographics" section, that the larger the sample size of a study, the more reliable its results. Relatedly, the larger the sample size of a study, the greater its ability to find if small effects are significant. A small change is less likely to be due to random fluctuations when found in a study with a thousand people, let's say, than in a study with ten people.

This explains why a meta-analysis may find significant changes by pooling the data of several studies which, independently, found no significant changes.

P-values 101

Most often, an effect is said to be significant if the statistical analysis (run by the researchers post-study) delivers a p-value that isn't higher than a certain threshold (set by the researchers pre-study). We'll call this threshold the threshold of significance.

Understanding how to interpret p-values correctly can be tricky, even for specialists, but here's an intuitive way to think about them:

Think about a coin toss. Flip a coin 100 times and you will get roughly a 50/50 split of heads and tails. Not terribly surprising. But what if you flip this coin 100 times and get heads every time? Now that's surprising! For the record, the probability of it actually happening is 0.00000000000000000000000000008%.

You can think of p-values in terms of getting all heads when flipping a coin.

• A p-value of 5% (p = 0.05) is no more surprising than getting all heads on 4 coin tosses.

• A p-value of 0.5% (p = 0.005) is no more surprising than getting all heads on 8 coin tosses.

• A p-value of 0.05% (p = 0.0005) is no more surprising than getting all heads on 11 coin tosses.

Contrary to popular belief, the "p" in "p-value" does not stand for "probability". The probability of getting 4 heads in a row is 6.25%, not 5%. If you want to convert a p-value into coin tosses (technically called S-values) and a probability percentage, check out the converter here.

As we saw, an effect is significant if the data collected over the course of the trial would be unlikely if there really was no effect. Now we can add that, the lower the p-value (under the threshold of significance), the more confident we can be that an effect is significant.

P-values 201

All right. Fair warning: we're going to get nerdy. Well, nerdier. Feel free to skip this section and resume reading here.

Still with us? All right, then — let's get at it. As we've seen, researchers run statistical analyses on the results of their study (usually one analysis per endpoint) in order to decide whether or not the intervention had an effect. They commonly make this decision based on the p-value of the results, which tells you how likely a result at least as large as the one observed would be if the null hypothesis, among other assumptions, were true.

Ah, jargon! Don't panic, we'll explain and illustrate those concepts.

In every experiment there are generally two opposing statements: the null hypothesis and the alternative hypothesis. Let's imagine a fictional study testing the weight-loss supplement "Better Weight" against a placebo. The two opposing statements would look like this:

• Null hypothesis: compared to placebo, Better Weight does not increase or decrease weight. (The hypothesis is that the supplement's effect on weight is null.)

• Alternative hypothesis: compared to placebo, Better Weight does decrease or increase weight. (The hypothesis is that the supplement has an effect, positive or negative, on weight.)

The purpose is to see whether the effect (here, on weight) of the intervention (here, a supplement called "Better Weight") is better, worse, or the same as the effect of the control (here, a placebo, but sometimes the control is another, well-studied intervention; for instance, a new drug can be studied against a reference drug).

For that purpose, the researchers usually set a threshold of significance (α) before the trial. If, at the end of the trial, the p-value (p) from the results is less than or equal to this threshold (p ≤ α), there is a significant difference between the effects of the two treatments studied. (Remember that, in this context, significant means statistically significant.)

Figure 5: Threshold for statistical significance

The most commonly used threshold of significance is 5% (α = 0.05). It means that if the null hypothesis (i.e., the idea that there was no difference between treatments) is true, then, after repeating the experiment an infinite number of times, the researchers would get a false positive (i.e., would detect a significant effect where there is none) at most 5% of the time (p ≤ 0.05).

Generally, the p-value is a measure of consistency between the results of the study and the idea that the two treatments have the same effect. Let's see how this would play out in our Better Weight weight-loss trial, where one of the treatments is a supplement and the other a placebo:

• Scenario 1: The p-value is 0.80 (p = 0.80). The results are more consistent with the null hypothesis (i.e., the idea that there is no difference between the two treatments). We conclude that Better Weight had no significant effect on weight loss compared to placebo.

• Scenario 2: The p-value is 0.01 (p = 0.01). The results are more consistent with the alternative hypothesis (i.e., the idea that there is a difference between the two treatments). We conclude that Better Weight had a significant effect on weight loss compared to placebo.

While p = 0.01 is a significant result, so is p = 0.000001. So what information do smaller p-values offer us? They give us greater confidence in the findings. In our example, a p-value of 0.000001 would give us greater confidence that Better Weight had a significant effect on weight change.

Remember that a significant effect may not be clinically relevant. Let's say that we found a significant result of p = 0.01 showing that Better Weight improves weight loss. The catch: Better Weight produced only 0.2 kg (0.5 lb) more weight loss compared to placebo after one year — a difference too small to have any meaningful effect on health. In this case, though the result is significant, statistically, the real-world effect is too small to justify taking this supplement. (This type of scenario is more likely to take place when the study is large since, as we saw, the larger the sample size of a study, the greater its ability to find if small effects are significant.)

Finally, we should mention that, though the most commonly used threshold of significance is 5% (p ≤ 0.05), some studies require greater certainty. For instance, for genetic epidemiologists to declare that a genetic association is statistically significant (say, to declare that a gene is associated with weight gain), the threshold of significance is usually set at 0.0000005% (p ≤ 0.000000005), which corresponds to getting all heads on 28 coin tosses. The probability of this happening is 0.00000003%.

P-values: Don't worship them!

Finally, keep in mind that, while important, p-values aren't the final say on whether a study's conclusions are accurate.

We saw that researchers too eager to find an effect in their study may resort to "data fishing". They may also try to lower p-values in various ways: for instance, they may run different analyses on the same data and only report the significant p-values, or they may recruit more and more participants until they get a statistically significant result. These bad scientific practices are known as "p-hacking" or "selective reporting". (You can read about a real-life example of this here.)

While a study's statistical analysis usually accounts for the variables the researchers were trying to control for, p-values can also be influenced (on purpose or not) by study design, hidden confounders, the types of statistical tests used, and much, much more. When evaluating the strength of a study's design, imagine yourself in the researcher's shoes and consider how you could torture a study to make it say what you want and advance your career in the process.

The Solar System Guided Reading and Study Answers

Source: https://examine.com/guides/how-to-read-a-study/

Bagikan Artikel ini